Additive & Spectral: IFFT Synthesis

The calculation of single sinusoidal components in the time domain can be very inefficient for a large number of partials. IFFT synthesis can be used to compose spectra in the frequency domain.

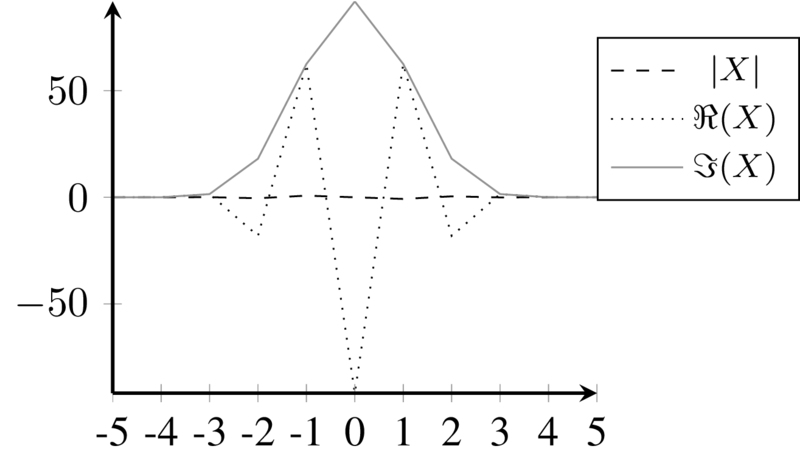
/images/Sound_Synthesis/ifft/ifft-0.png

Main lobe kernel for \(\varphi = 0\)

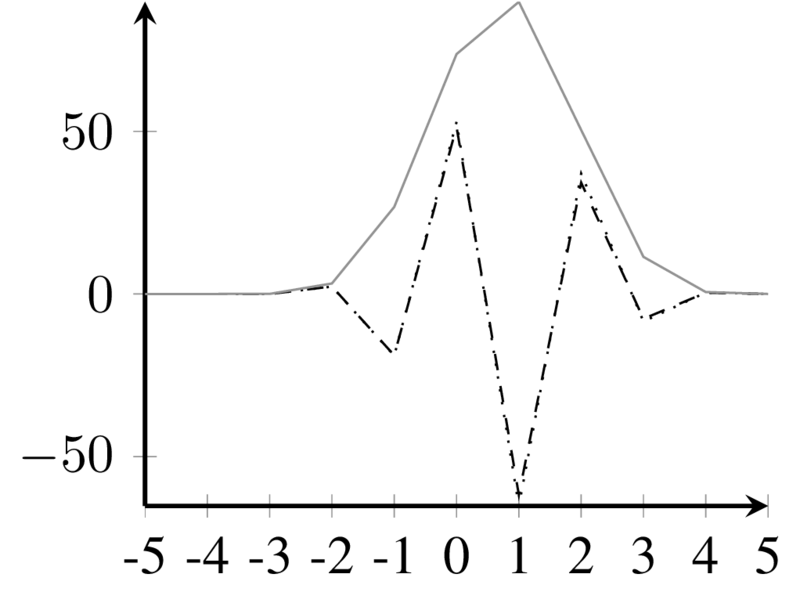
/images/Sound_Synthesis/ifft/ifft-1.png

Main lobe kernel for \(\varphi = \pi/2\)

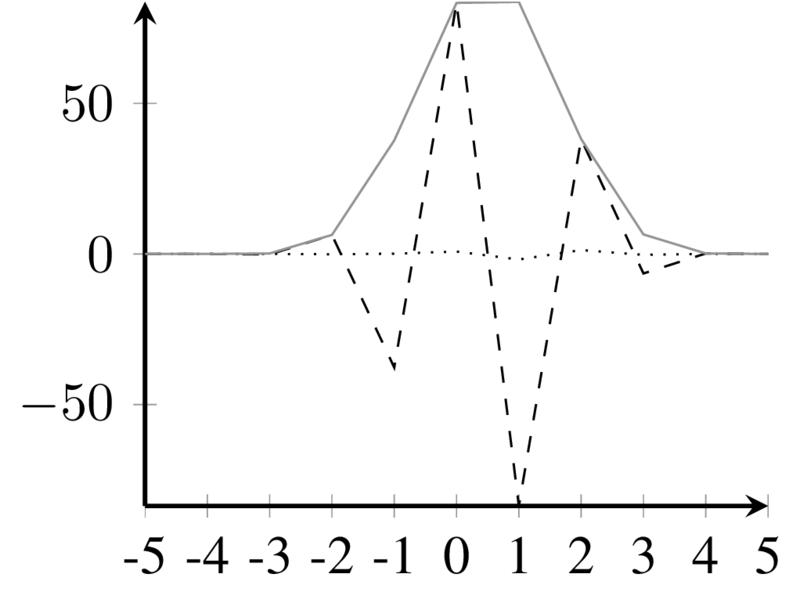
/images/Sound_Synthesis/ifft/ifft-2.png

Main lobe kernel for \(\varphi = \pi/4\)

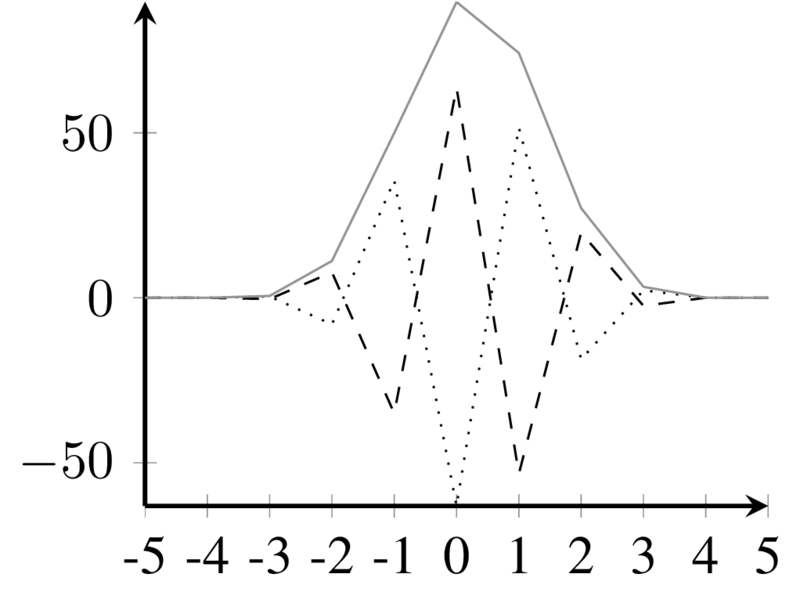
/images/Sound_Synthesis/ifft/ifft-3.png

Main lobe kernel for \(\varphi =c3 \pi/4\)