Additive & Spectral: Spectral Modeling

McAulay/Quatieri

Sinusoidal modeling can be considered a higher level algorithm for the additive synthesis of harmonic sounds. It has first been used in speech processing by McAulay, R. and Quatieri (1986). For low framerates they proposed a time-domain method for partial synthesis with original phases of the partials.

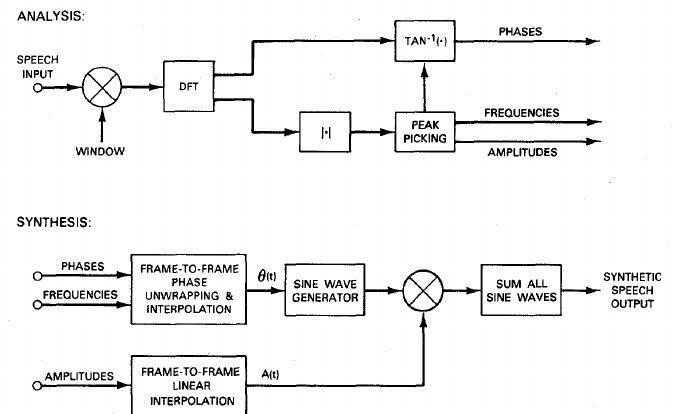
/images/Sound_Synthesis/spectral_modeling/quatieri_system.jpg — *R. McAulay and T. Quatieri (1986)*

SMS

The above presented sinusoidal modeling approach captures only the harmonic portion of a sound. With the Sinusoids plus Noise model (SMS), Serra and Smith (1990) introduced the Deterministic + Stochastic model for spectral modeling, in order to model components in the signal which are not captured by partial tracking. A sound is therefor modeled as a combination of a dererministic component - the sinusoids - and a stochasctic component:

\begin{equation*} x = x_{DET} + x_{STO} \end{equation*}

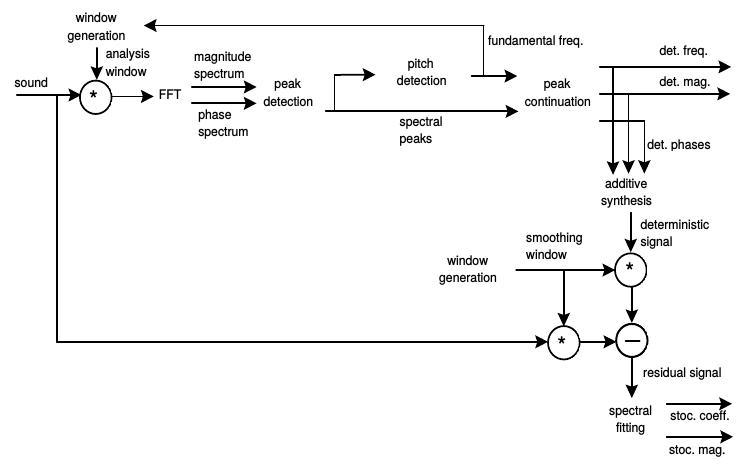
/images/Sound_Synthesis/spectral_modeling/sines_plus_noise_block.jpg — *Deterministic + Stochastic model (Serra and Smith, 1990)*

Violin Example

The following example shows the sines + noise decomposition for a single violin sound. The original recording was made in an anechoic chamber:

After partial tracking, the deterministic component can be re-synthesized using an oscillator bank. It features the strings oscillation, in this case with original phases. For a bowed string instrument like the violin, the deterministic model alone can deliver plausible results:

The residual signal still carries some parts of the deterministic part, when calculated with simple subtraction. Most of the residual's energy is caused by the bow friction:

Sines + Transients + Noise

Even the harmonic and noise model can not capture all components of musical sounds. The third - and in this line last - signal component to be included are the transients.

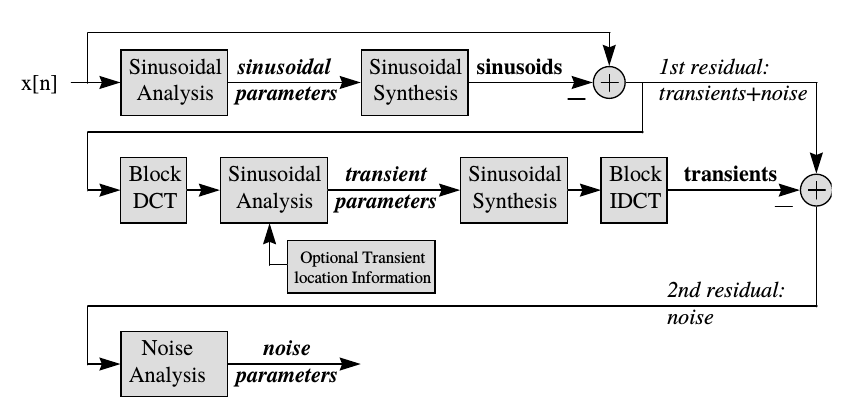
/images/Sound_Synthesis/spectral_modeling/sin-trans-noise.png — *Sines + Transients + Noise (Levine and Smith, 1998)*

References

2007

Arturo Camacho. Swipe: A Sawtooth Waveform Inspired Pitch Estimator for Speech and Music. PhD thesis, University of Florida, Gainesville, FL, USA, 2007.
[details] [BibTeX▼]

@phdthesis{camacho2007asawtooth,
    author = "Camacho, Arturo",
    address = "Gainesville, FL, USA",
    advisor = "Harris, John G.",
    school = "University of Florida",
    title = "{Swipe: A Sawtooth Waveform Inspired Pitch Estimator for Speech and Music}",
    year = "2007"
}

2005

Julius O. Smith and Xavier Serra. PARSHL: An Analysis/Synthesis Program for Non-Harmonic Sounds Based on a Sinusoidal Representation. In Proceedings of the International Computer Music Conference (ICMC). Barcelona, Spain, 2005. URL: http://www.bibsonomy.org/bibtex/2fa00c44d6ff2549f4d0559a105631fd7/zazi.
[details] [BibTeX▼]

@inproceedings{Smith2005parshl,
    author = "Smith, Julius O. and Serra, Xavier",
    title = "{PARSHL: An Analysis/Synthesis Program for Non-Harmonic Sounds Based on a Sinusoidal Representation}",
    booktitle = "{Proceedings of the International Computer Music Conference (ICMC)}",
    year = "2005",
    address = "Barcelona, Spain",
    keywords = "imported",
    owner = "zazi",
    timestamp = "2010-01-28T22:00:35.000+0100",
    url = "http://www.bibsonomy.org/bibtex/2fa00c44d6ff2549f4d0559a105631fd7/zazi"
}

2002

Alain de Cheveigné and Hideki Kawahara. YIN, a Fundamental Frequency Estimator for Speech and Music. The Journal of the Acoustical Society of America, 111(4):1917–1930, 2002.
[details] [BibTeX▼]

@article{decheveigne2002yin,
    author = "de Cheveigné, Alain and Kawahara, Hideki",
    journal = "The Journal of the Acoustical Society of America",
    keywords = "guitar",
    number = "4",
    pages = "1917–1930",
    posted-at = "2010-10-04 09:51:23",
    publisher = "ASA",
    title = "{YIN, a Fundamental Frequency Estimator for Speech and Music}",
    volume = "111",
    year = "2002"
}

1998

Scott Levine and Julius Smith. A Sines + Transients + Noise Audio Representation for Data Compression and Time/Pitch Scale Modifications. In Proceedings of the 105th Audio Engineering Society Convention. San Francisco, CA, 1998.
[details] [BibTeX▼]

@inproceedings{levine1998asines,
    author = "Levine, Scott and Smith, Julius",
    title = "{A Sines + Transients + Noise Audio Representation for Data Compression and Time/Pitch Scale Modifications}",
    booktitle = "{Proceedings of the 105th Audio Engineering Society Convention}",
    year = "1998",
    address = "San Francisco, CA"
}

1990

Xavier Serra and Julius Smith. Spectral Modeling Synthesis: A Sound Analysis/Synthesis System Based on a Deterministic Plus Stochastic Decomposition . Computer Music Journal, 14(4):12–14, 1990.
[details] [BibTeX▼]

@article{Serra1990spectralmodeling,
    author = "Serra, Xavier and Smith, Julius",
    journal = "Computer Music Journal",
    number = "4",
    pages = "12–14",
    publisher = "MIT Press",
    title = "{Spectral Modeling Synthesis: A Sound Analysis/Synthesis System Based on a Deterministic Plus Stochastic Decomposition }",
    volume = "14",
    year = "1990"
}

1986

R. McAulay and T. Quatieri. Speech analysis/Synthesis based on a sinusoidal representation. Acoustics, Speech and Signal Processing, IEEE Transactions on, 34(4):744–754, 1986.
[details] [BibTeX▼]

@article{McAulay1986,
    author = "McAulay, R. and Quatieri, T.",
    journal = "Acoustics, Speech and Signal Processing, IEEE Transactions on",
    number = "4",
    pages = "744–754",
    title = "{Speech analysis/Synthesis based on a sinusoidal representation}",
    volume = "34",
    year = "1986"
}

T Quatieri and Rl McAulay. Speech transformations based on a sinusoidal representation. IEEE Transactions on Acoustics, Speech, and Signal Processing, 34(6):1449–1464, 1986.
[details] [BibTeX▼]

@article{quatieri1986speech,
    author = "Quatieri, T and McAulay, Rl",
    journal = "IEEE Transactions on Acoustics, Speech, and Signal Processing",
    number = "6",
    pages = "1449–1464",
    publisher = "IEEE",
    title = "{Speech transformations based on a sinusoidal representation}",
    volume = "34",
    year = "1986"
}