Understanding Ambisonics Signals

Spherical Harmonics

Ambisonics is based on a decomposition of a sound field into spherical harmonics. These spherical harmonics encode the sound field according to different axes, respectively angles of incidence. The number of Ambisonics channels $N$ is equal to the number of spherical harmonics. It can be calculated for a given order $M$ with the following formula:

\begin{equation*} N = (M+1)^2 \end{equation*}

Figure 1 shows the first 16 spherical harmonics. The first row ($N=1$) is the omnidirectional sound pressure for the order $M=0$. Rows 1-2 together represent the $N=4$ spherical harmonics of the first order Ambisonics signal, rows 1-3 correspond to $M=2$, respectively $N=9$ and rows 1-4 to the third order Ambisonics signal with $N=16$ spherical harmonics. First order ambisonics is sufficient to encode a threedimensional sound field. The higher the Ambisonics order, the more precise the directional encoding.

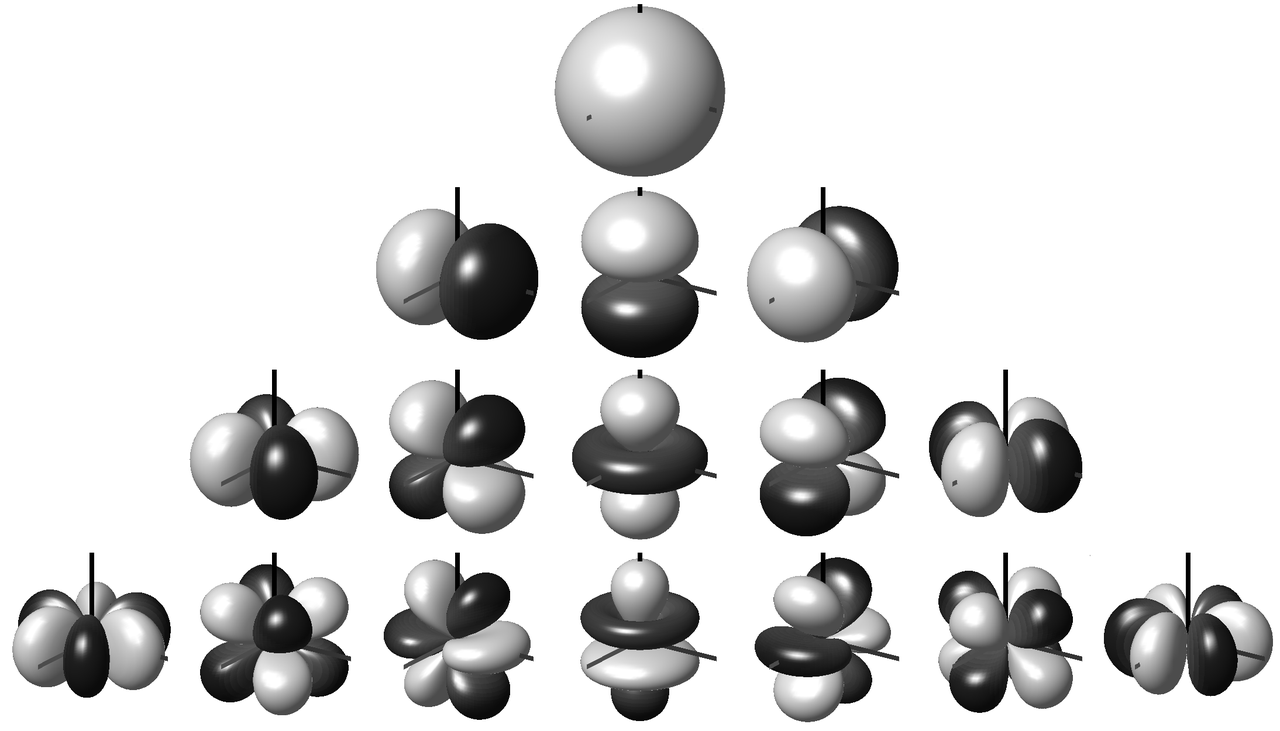
/images/spatial/ambisonics/third-order-ambisonics.png

Fig. 1: Spherical harmonics up to order 3 [1].

Ambisonic Formats

An Ambisonics B Format file or signal carries all $N$ spherical harmonics. Figure 2 shows a first order B Format signal.

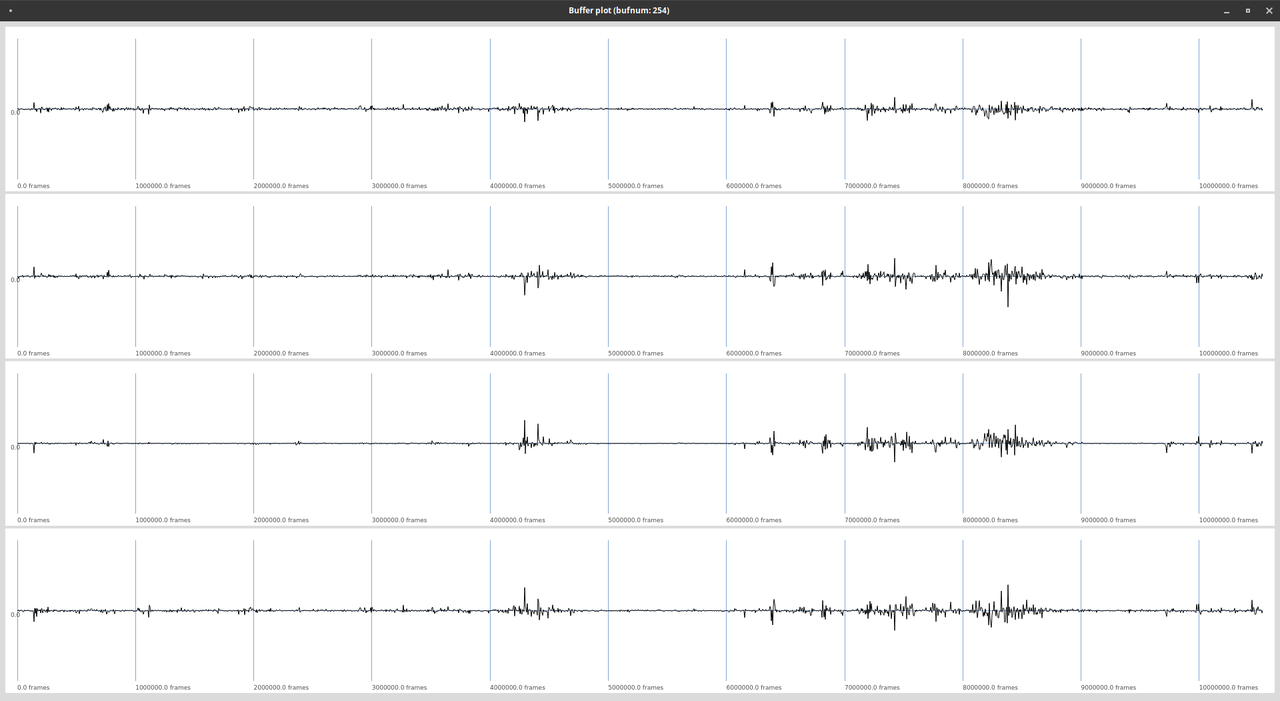
/images/spatial/ambisonics/first-order-signal.png

Fig. 2: Four channels of a first order Ambisonics signal.

There are different conventions for the sequence of the individual signals, as well as for the normalization.

References

2015

  • Matthias Frank, Franz Zotter, and Alois Sontacchi. Producing 3d audio in ambisonics. In Audio Engineering Society Conference: 57th International Conference: The Future of Audio Entertainment Technology–Cinema, Television and the Internet. Audio Engineering Society, 2015.
    [details] [BibTeX▼]

2009

  • Frank Melchior, Andreas Gräfe, and Andreas Partzsch. Spatial audio authoring for ambisonics reproduction. In Proc. of the Ambisonics Symposium. 2009.
    [details] [BibTeX▼]