Additive & Spectral: Studie 2

The history of Elektronische Musik started with additive synthesis. In his composition Studie II, Karlheinz Stockhausen composed timbres by superimposing sinusoidal components. In that era this was realized through single sine wave oscillators, tuned to the desired frequency and recorded on tape.

The Score

Studie II is the attempt to fully compose music on a timbral level in a rigid score. Stockhausen therefor generated tables with frequencies and mixed tones for creating source material. Fig.1 shows an excerpt from the timeline, which was used to arrange the material. The timbres are recognizable through their vertical position in the upper system, whereas the lower system represents articulation, respectively fades and amplitudes.

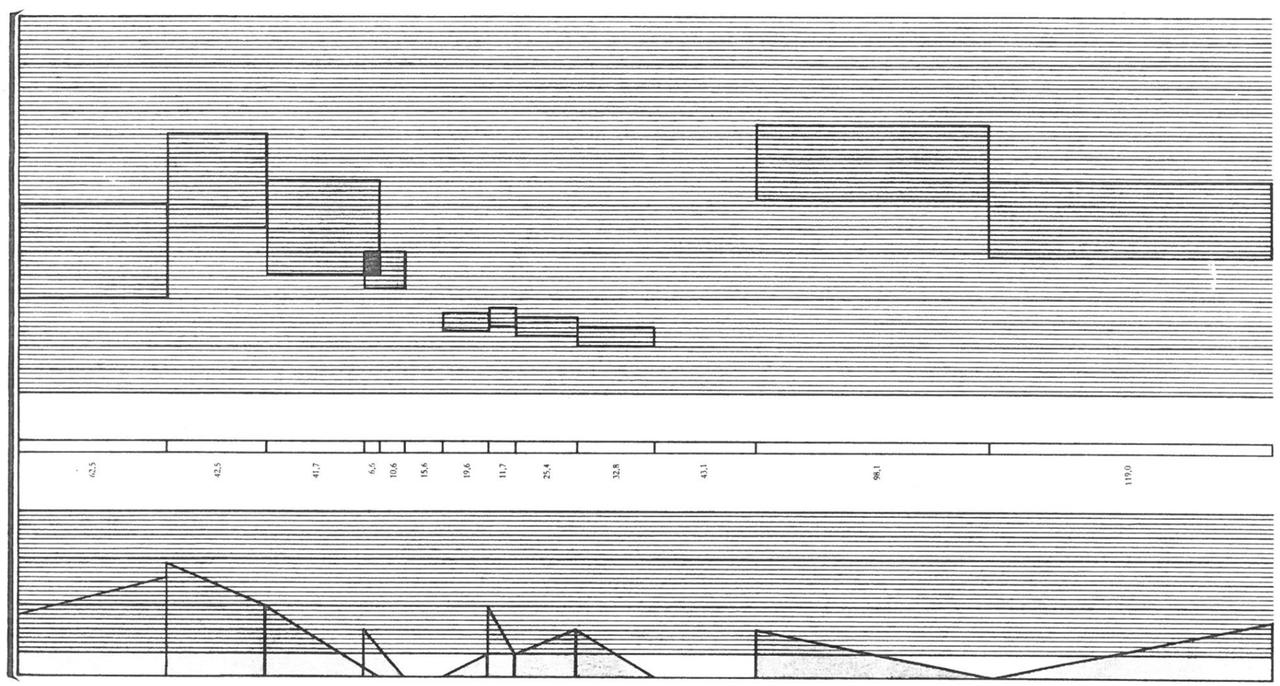
/images/Sound_Synthesis/studie4.jpg

Fig.1: From the score of Studie II.

The Scale

Central Interval

For Studie II, Stockhausen created a frequency scale, which not only affects the fundamental frequencies but also the overtone structure of all sounds which can be represented by this scale. He chose a central interval, based on the following formula:

\begin{equation*} \sqrt[25]{5} = 1.0665 \end{equation*}

This odd interval has 25 equally spaced pitches in 4 octaves. It is slightly higher than the semitone in the equal temperament, which has 12 equally spaced pitches in one octave:

\begin{equation*} \sqrt[12]{2} = 1.0595 \end{equation*}

Interval Comparison

The following buttons play both intervals starting at 443 Hz for a comparison. The difference is minute but can be detected by trained ears:

Pitch Scale

Stockhausen used the \(\sqrt[25]{5}\) interval to create a pitch scale. Starting from a root pitch of $100$ Hz, the scale ascends in 80 \(\sqrt[25]{5}\) steps. However, the highest pitch value used for composing timbres lies at:

\begin{equation*} \displaystyle 100 \mathrm{\ Hz\ } (\sqrt[25]{5})^{60} = 4759.13 \mathrm{Hz} \end{equation*}

The Timbres

From the 81 frequencies in the pitch scale, Stockhausen creates 5 different timbres - in German Tongemische. Each timbre is based on the \(\sqrt[25]{5}\) interval but with five different spread factors, namely 1,2,3,4 and 5. The following table shows all five timbres for the base frequency of 100 Hz, with the spread factor in the exponent:

Timbres for 100 Hz Base Frequency.

Partial Ratio

Partial 1 [Hz]

Partial 2 [Hz]

Partial 3 [Hz]

Partial 4 [Hz]

Partial 5 [Hz]

Timbre 1

\((\sqrt[25]{5})^1\)

100.00

106.65

113.74

121.30

129.37

Timbre 2

\((\sqrt[25]{5})^2\)

100.00

113.74

129.37

147.15

167.37

Timbre 3

\((\sqrt[25]{5})^3\)

100.00

121.30

147.15

178.50

216.52

Timbre 4

\((\sqrt[25]{5})^4\)

100.00

129.37

167.37

216.52

280.12

Timbre 5

\((\sqrt[25]{5})^5\)

100.00

137.97

190.37

262.65

362.39

Pitch (Hz):

Spacing Factor:

1 2 3 4 5

P1 (Hz):

P2 (Hz):

P3 (Hz):

P4 (Hz):

P5 (Hz):

Output Gain:

Duration (seconds):

Envelope:

Time Domain:

Frequency Domain:

References

1998

  • Agostino Di Scipio. Compositional models in xenakis's electroacoustic music. Perspectives of New Music, pages 201–243, 1998.
    [details] [BibTeX▼]

1870

  • Hermann von Helmholtz. Die Lehre von den Tonempfindungen als physiologische Grundlage für die Theorie der Musik, 3. umgearbeitete Ausgabe. Braunschweig: Vieweg, 1870.
    [details] [BibTeX▼]