Understanding Ambisonics

A vs B Format

A-format refers to the raw microphone capsule signals (e.g., tetrahedral mic outputs) when capturing 3D sound fields. This format is mic-specific and not interchangeable. To further process it, it usually needs to be converted to B-format. A→B conversion matrices are microphone-model-specific, considering capsule geometry and calibration. Microphone vendors need to supply the decoder.

/images/spatial/ambisonics/ambisonics_capsule.png

B-format is made up of the spherical-harmonic components of the sound field. This is the standard Ambisonics format with defined channel order and normalization. B-format is portable and can be reproduced on any rendering system (loudspeaker setups, binaural), following standardized decoding algorithms.

Spherical Harmonics

Basic Ambisonics does not define a sound filed through positions, but through angles of incedence. Ambisonics is based on a decomposition of a sound field into spherical harmonics and dates back to Gerzon's theory of Peryphony (Gerzon, 1973). These spherical harmonics encode a sound field into to different axes, The number of Ambisonics channels $N$ is equal to the number of spherical harmonics. It can be calculated for a given order $M$ with the following formula:

\begin{equation*} N = (M+1)^2 \end{equation*}

Figure 1 shows the first 16 spherical harmonics. The first row ($N=1$) is the omnidirectional sound pressure for the order $M=0$.

  • Rows 1-2 together represent the $N=4$ spherical harmonics of the first order Ambisonics signal.

  • Rows 1-3 correspond to $M=2$, respectively $N=9$.

  • Rows 1-4 to the third order Ambisonics signal with $N=16$ spherical harmonics.

First order ambisonics is sufficient to encode a threedimensional sound field. The higher the Ambisonics order, the more precise the directional encoding and the better the localization of virtual sound sources.

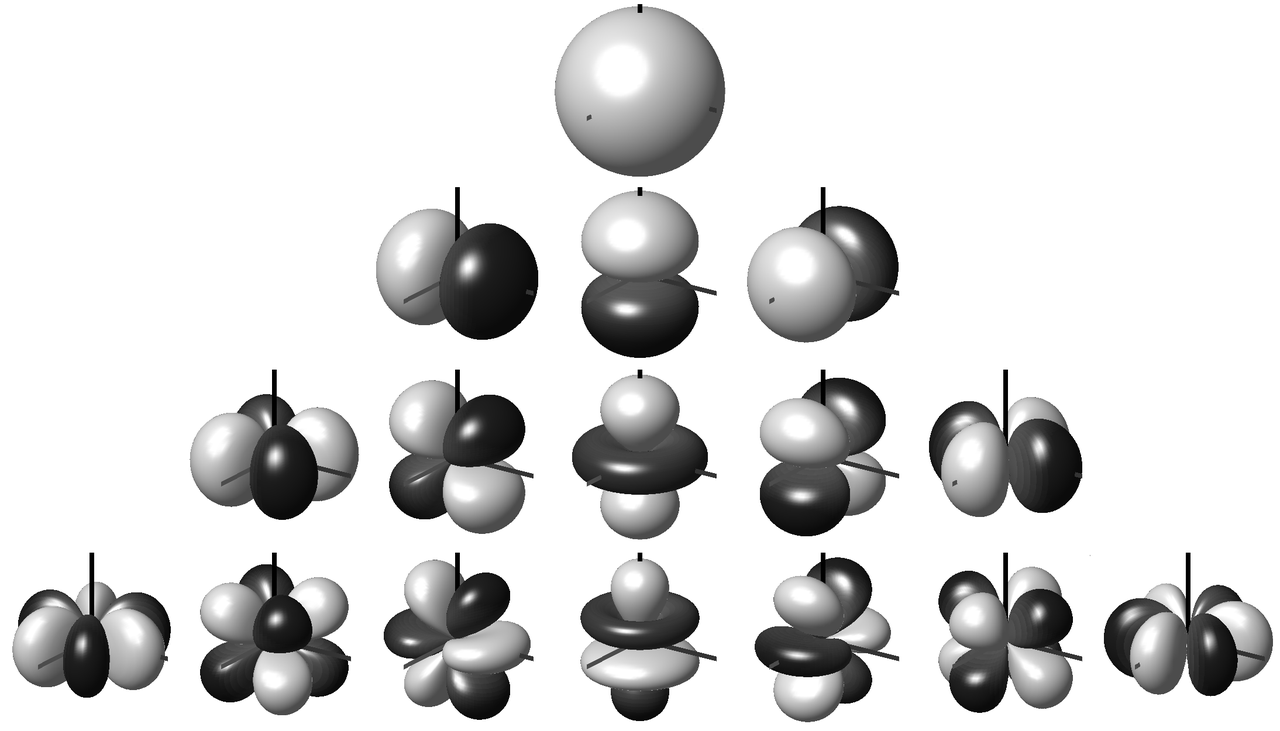
/images/spatial/ambisonics/third-order-ambisonics.png

Fig. 1: Spherical harmonics up to order 3 [1].

Common B-format Conventions

B-format conventions define the relation between Ambisonic channel order and spherical harmonics. There are different conventions for the sequence of the individual signals, as well as for the normalization.

Ambisonics conventions (Common B-format variants)
Convention Type Channel order (1st order) Normalization Notes / Where used
FuMa (Furse–Malham) B-format (FOA) W, X, Y, Z FuMa (“maxN” style; W is scaled by 1/√2) Legacy 1st-order B-format used in older DAWs and toolchains; awkward for higher orders (≥2).
AmbiX B-format (FOA/HOA) ACN order → [0:W, 1:Y, 2:Z, 3:X] SN3D De-facto modern production standard (Reaper+AmbiX, many VR/AR SDKs, YouTube VR). Portable and HOA-friendly.
ACN/N3D B-format (FOA/HOA) ACN order → [0:W, 1:Y, 2:Z, 3:X] N3D (orthonormal) Common in research and HOA libraries; convenient for math/analysis and per-order processing.

Ambisonic Formats

An Ambisonics B Format file or signal carries all $N$ spherical harmonics. Figure 2 shows a first order B Format signal.

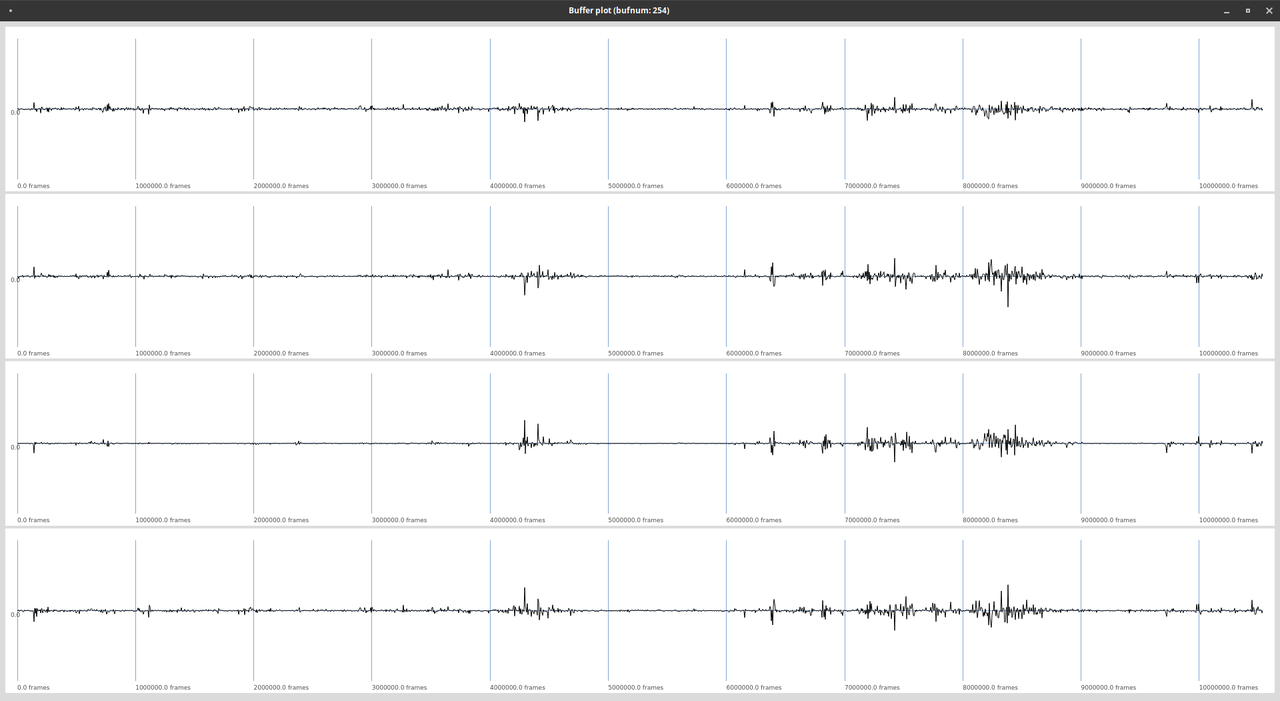
/images/spatial/ambisonics/first-order-signal.png

Fig. 2: Four channels of a first order Ambisonics signal.

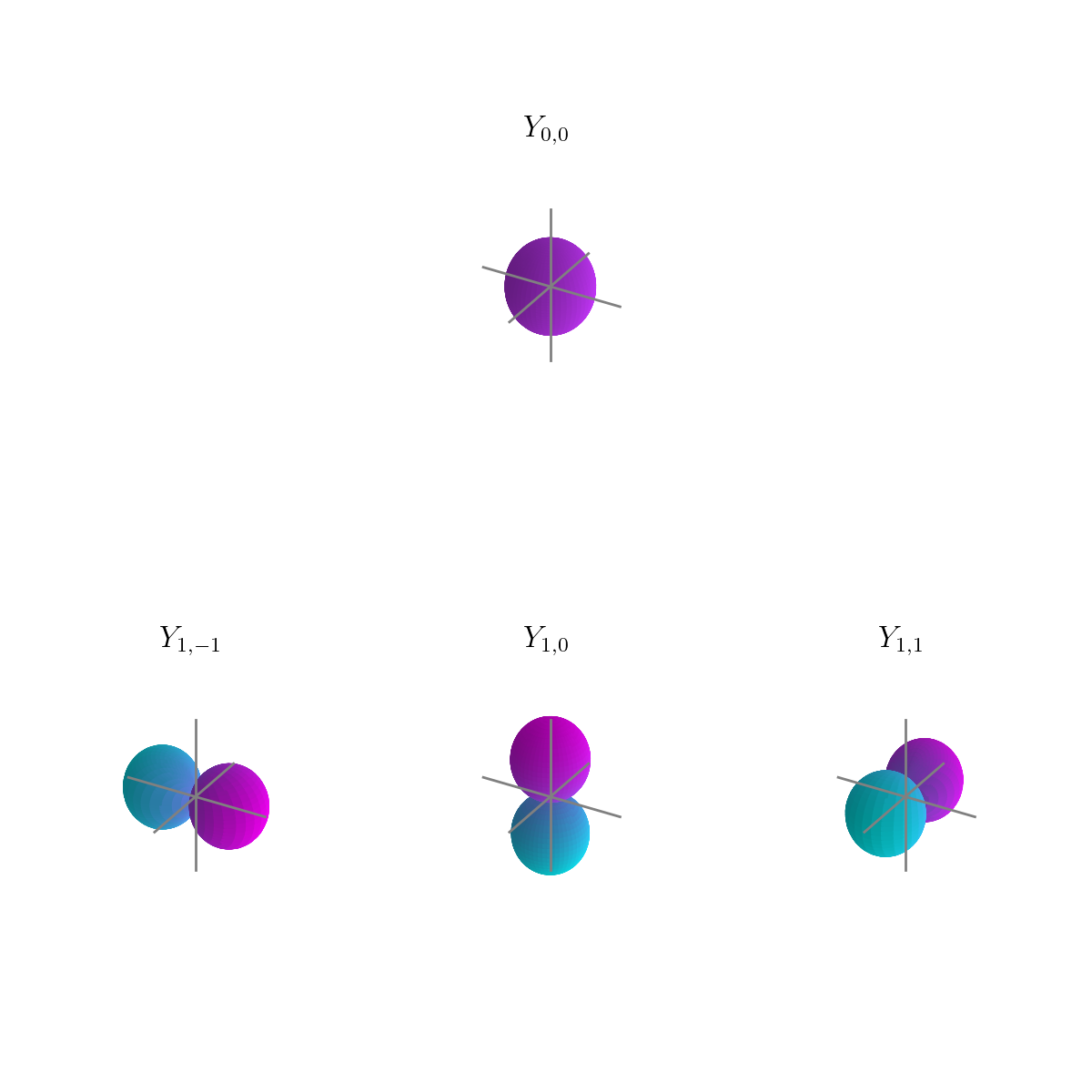
/images/spatial/ambisonics/first-order-harmonics.png

Fig. 2: Spherical harmonics of a first order Ambisonics signal.

ACN, Normalizations, and 1st-Order Mappings

ACN (Ambisonic Channel Numbering)

The channel index \(n\) is

\begin{equation*} n = \ell(\ell+1) + m, \qquad \ell = 0..L,\ \ m = -\ell..\ell. \end{equation*}

For 1st order (\(\ell = 0,1\)), the ACN indices map to channels as

\begin{equation*} [\,0:\ Y_0^0 = W,\quad 1:\ Y_1^{-1} = Y,\quad 2:\ Y_1^{0} = Z,\quad 3:\ Y_1^{1} = X\,]. \end{equation*}

Normalizations

  • SN3D (“semi-normalized”): \(Y_0^0 = 1\). Widely used in production (AmbiX).

  • N3D (orthonormal over the sphere): convenient for HOA math/analysis.

  • FuMa (legacy): distinct scaling; notably \(W_{\text{FuMa}} = \tfrac{1}{\sqrt{2}}\,W_{\text{SN3D}}\).

1st-Order Mappings (FuMa ↔ AmbiX/ACN–SN3D)

Channel order

  • FuMa order: [W, X, Y, Z]

  • AmbiX (ACN/SN3D) order: [W, Y, Z, X] (i.e., ACN indices [0,1,2,3] -> [W,Y,Z,X])

References

2019

  • Franz Zotter and Matthias Frank. Ambisonics: A Practical 3D Audio Theory for Recording, Studio Production, Sound Reinforcement, and Virtual Reality. Springer, 2019.
    [details] [BibTeX▼]

2015

  • Matthias Frank, Franz Zotter, and Alois Sontacchi. Producing 3d audio in ambisonics. In Audio Engineering Society Conference: 57th International Conference: The Future of Audio Entertainment Technology–Cinema, Television and the Internet. Audio Engineering Society, 2015.
    [details] [BibTeX▼]

2009

  • Frank Melchior, Andreas Gräfe, and Andreas Partzsch. Spatial audio authoring for ambisonics reproduction. In Proc. of the Ambisonics Symposium. 2009.
    [details] [BibTeX▼]

1973

  • Michael A. Gerzon. Periphony: With-Height Sound Reproduction. Journal of the Audio Engineering Society, 21(1):2–10, 1973.
    [details] [BibTeX▼]