Understanding Ambisonics Signals

Spherical Harmonics

Ambisonics is based on a decomposition of a sound field into spherical harmonics. These spherical harmonics encode the sound field according to different axes, respectively angles of incidence. The number of Ambisonics channels $N$ is equal to the number of spherical harmonics. It can be calculated for a given order $M$ with the following formula:

\begin{equation*} N = (M+1)^2 \end{equation*}

Figure 1 shows the first 16 spherical harmonics. The first row ($N=1$) is the omnidirectional sound pressure for the order $M=0$. Rows 1-2 together represent the $N=4$ spherical harmonics of the first order Ambisonics signal, rows 1-3 correspond to $M=2$, respectively $N=9$ and rows 1-4 to the third order Ambisonics signal with $N=16$ spherical harmonics. First order ambisonics is sufficient to encode a threedimensional sound field. The higher the Ambisonics order, the more precise the directional encoding.

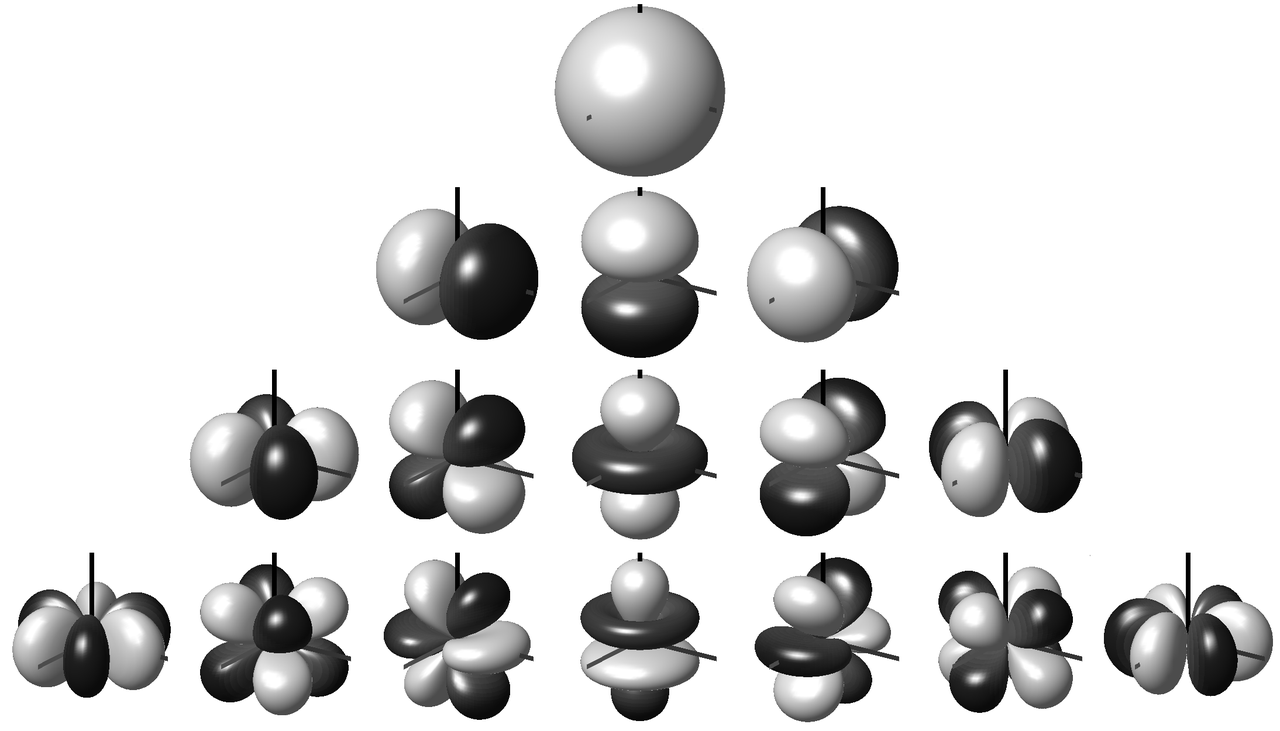
/images/spatial/ambisonics/third-order-ambisonics.png

Fig. 1: Spherical harmonics up to order 3 [1].

Ambisonic Formats

An Ambisonics B Format file or signal carries all $N$ spherical harmonics. Figure 2 shows a first order B Format signal.

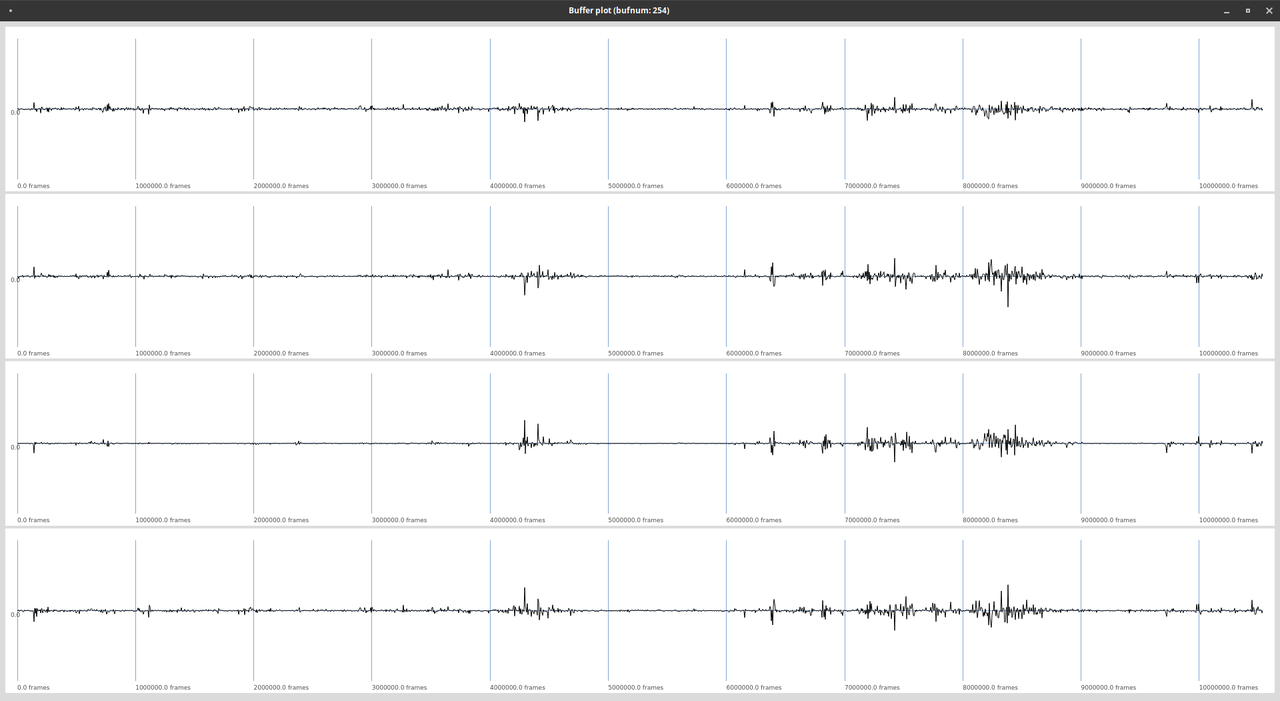
/images/spatial/ambisonics/first-order-signal.png

Fig. 2: Four channels of a first order Ambisonics signal.

There are different conventions for the sequence of the individual signals, as well as for the normalization.

FOA / HOA Encoding from Angular Direction

Conventions

  • Coordinates: \(x=\text{front}\), \(y=\text{left}\), \(z=\text{up}\).

  • Angles: azimuth \(\varphi \in (-\pi, \pi]\) (CCW from +x toward +y), elevation \(\theta \in [-\pi/2, \pi/2]\) (up from horizontal plane).

  • Normalisation/order: AmbiX (ACN channel order, SN3D normalisation), unless noted. ACN index \(n=\ell(\ell+1)+m\). For FOA (order \(\ell=1\)), the mapping is \([n]=[0,1,2,3] \leftrightarrow [W,Y,Z,X]\).

First-Order Ambisonics (FOA, B-format) — Single Point Source

A monophonic source \(s(t)\) at direction \((\varphi,\theta)\) encodes to the FOA vector \(\mathbf a(t)=\begin{bmatrix}W&Y&Z&X\end{bmatrix}^{\mathsf T}\) (AmbiX ordering) as:

\begin{equation*} \begin{aligned} W(t) &= s(t)\,Y_0^0(\theta,\varphi),\\ Y(t) &= s(t)\,Y_1^{-1}(\theta,\varphi),\\ Z(t) &= s(t)\,Y_1^{0}(\theta,\varphi),\\ X(t) &= s(t)\,Y_1^{1}(\theta,\varphi), \end{aligned} \end{equation*}

with the real SN3D first-order spherical harmonics:

\begin{equation*} \boxed{ \begin{aligned} Y_0^0(\theta,\varphi) &= 1,\\ Y_1^{1}(\theta,\varphi) &= \cos\theta\,\cos\varphi,\\ Y_1^{-1}(\theta,\varphi) &= \cos\theta\,\sin\varphi,\\ Y_1^{0}(\theta,\varphi) &= \sin\theta. \end{aligned} } \end{equation*}

Thus, explicitly:

\begin{equation*} \boxed{ \begin{aligned} W(t) &= s(t),\\ X(t) &= s(t)\,\cos\theta\,\cos\varphi,\\ Y(t) &= s(t)\,\cos\theta\,\sin\varphi,\\ Z(t) &= s(t)\,\sin\theta. \end{aligned} } \end{equation*}

FuMa (legacy) mapping (if required):

\begin{equation*} \boxed{ \begin{aligned} W_{\mathrm{FuMa}}(t) &= \tfrac{1}{\sqrt{2}}\,s(t),\\ X_{\mathrm{FuMa}}(t) &= s(t)\,\cos\theta\,\cos\varphi,\\ Y_{\mathrm{FuMa}}(t) &= s(t)\,\cos\theta\,\sin\varphi,\\ Z_{\mathrm{FuMa}}(t) &= s(t)\,\sin\theta. \end{aligned} } \end{equation*}

FOA — Multiple Point Sources (Object-Based)

For \(N\) sources \(s_i(t)\) at \((\varphi_i,\theta_i)\), FOA channels are a linear sum:

\begin{equation*} \boxed{ \mathbf a(t) = \sum_{i=1}^{N} s_i(t)\, \begin{bmatrix} 1\\[2pt] \cos\theta_i\,\sin\varphi_i\\[2pt] \sin\theta_i\\[2pt] \cos\theta_i\,\cos\varphi_i \end{bmatrix} \quad \text{(AmbiX/ACN order } [W,Y,Z,X]\text{).} } \end{equation*}

Higher-Order Ambisonics (General Order \(L\))

Let \(Y_{\ell}^{m}(\theta,\varphi)\) be the real SN3D spherical harmonics with \(\ell=0..L\) and \(m=-\ell..\ell\). For a single source:

\begin{equation*} \boxed{ a_{\ell m}(t) = s(t)\,Y_{\ell}^{m}(\theta,\varphi),\qquad \ell=0..L,\; m=-\ell..\ell. } \end{equation*}

For \(N\) sources:

\begin{equation*} \boxed{ a_{\ell m}(t) = \sum_{i=1}^{N} s_i(t)\,Y_{\ell}^{m}\!\bigl(\theta_i,\varphi_i\bigr). } \end{equation*}

Real SN3D Spherical Harmonics (Definition)

With associated Legendre functions \(P_\ell^m(\cdot)\) and SN3D factor \(N_{\ell m}=\sqrt{\dfrac{(2-\delta_{m0})(\ell-m)!}{(\ell+m)!}}\):

\begin{equation*} \boxed{ Y_\ell^{m}(\theta,\varphi)= \begin{cases} N_{\ell 0}\,P_\ell(\sin\theta), & m=0,\\[6pt] N_{\ell m}\,P_\ell^{m}(\sin\theta)\,\sqrt{2}\,\cos(m\varphi), & m>0,\\[6pt] N_{\ell |m|}\,P_\ell^{|m|}(\sin\theta)\,\sqrt{2}\,\sin(|m|\varphi), & m<0. \end{cases} } \end{equation*}

Notes

  • Plane-wave (far-field) model assumed; for finite distance, multiply by a radial factor \(R_\ell(kr)\) (e.g., NFC-HOA).

  • For head-tracked playback, rotate the Ambisonic channel vector per order using the spherical-harmonic rotation matrices \(\mathbf D_\ell(\cdot)\) before rendering.

References

2015

  • Matthias Frank, Franz Zotter, and Alois Sontacchi. Producing 3d audio in ambisonics. In Audio Engineering Society Conference: 57th International Conference: The Future of Audio Entertainment Technology–Cinema, Television and the Internet. Audio Engineering Society, 2015.
    [details] [BibTeX▼]

2009

  • Frank Melchior, Andreas Gräfe, and Andreas Partzsch. Spatial audio authoring for ambisonics reproduction. In Proc. of the Ambisonics Symposium. 2009.
    [details] [BibTeX▼]