VBAP

VBAP: Vector Base Amplitude Panning

Vector Base Amplitude Panning (VBAP) is a geometric amplitude panning method in which a virtual source direction is expressed as a linear combination of loudspeaker direction vectors (Pulkki, 1997). Only the minimum number of loudspeakers required to span the space are active to create one sound source - referred to as the base:

  • 2 loudspeakers in 2D

  • Three loudspeakers in 3D.

Algorithm (2D)

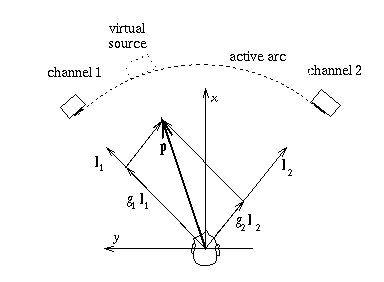
VBAP 2D principle

VBAP in two dimensions: a virtual source direction is expressed as a weighted combination of two loudspeaker direction vectors forming an active base (from the original VBAP docs: http://impala.utopia.free.fr/pd/patchs/externals_libs/vbap/vbap.html).

Let two loudspeakers define a panning base with unit direction vectors

\begin{equation*} \mathbf{l}_1 = \begin{bmatrix} \cos\theta_1 \\ \sin\theta_1 \end{bmatrix}, \qquad \mathbf{l}_2 = \begin{bmatrix} \cos\theta_2 \\ \sin\theta_2 \end{bmatrix} \end{equation*}

and a desired source direction

\begin{equation*} \mathbf{s} = \begin{bmatrix} \cos\theta \\ \sin\theta \end{bmatrix}. \end{equation*}

Form the loudspeaker matrix

\begin{equation*} \mathbf{L} = \begin{bmatrix} \mathbf{l}_1 & \mathbf{l}_2 \end{bmatrix}. \end{equation*}

The gain vector is obtained by

\begin{equation*} \mathbf{g} = \mathbf{L}^{-1}\mathbf{s} = \begin{bmatrix} g_1 \\ g_2 \end{bmatrix}. \end{equation*}

Energy normalization is applied to preserve constant power (Pulkki, 1997):

\begin{equation*} \mathbf{g} \leftarrow \frac{\mathbf{g}}{\sqrt{g_1^2 + g_2^2}}. \end{equation*}

Only bases for which \(g_i \ge 0\) are considered valid.

Algorithm (3D)

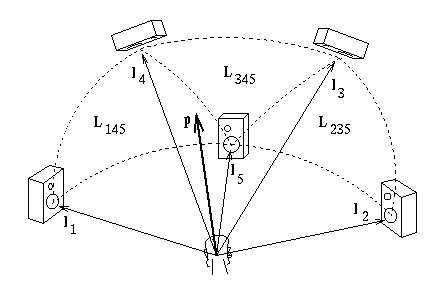
VBAP 3D principle

VBAP in three dimensions: loudspeaker triplets tessellate the sphere. One triplet is active at a time, defining a local panning base (from the original VBAP docs: http://impala.utopia.free.fr/pd/patchs/externals_libs/vbap/vbap.html).

In 3D, VBAP operates on loudspeaker triplets that form a tessellation of the unit sphere (Pulkki, 1999). Each loudspeaker direction is represented as a unit vector

\begin{equation*} \mathbf{l}_i = \begin{bmatrix} \cos\phi_i \cos\theta_i \\ \cos\phi_i \sin\theta_i \\ \sin\phi_i \end{bmatrix}. \end{equation*}

For a given triplet \((\mathbf{l}_1,\mathbf{l}_2,\mathbf{l}_3)\):

\begin{equation*} \mathbf{L} = \begin{bmatrix} \mathbf{l}_1 & \mathbf{l}_2 & \mathbf{l}_3 \end{bmatrix}, \end{equation*}

and the desired source direction

\begin{equation*} \mathbf{s} = \begin{bmatrix} \cos\phi \cos\theta \\ \cos\phi \sin\theta \\ \sin\phi \end{bmatrix}. \end{equation*}

The gain vector is computed as

\begin{equation*} \mathbf{g} = \mathbf{L}^{-1}\mathbf{s} = \begin{bmatrix} g_1 \\ g_2 \\ g_3 \end{bmatrix}, \end{equation*}

followed by normalization:

\begin{equation*} \mathbf{g} \leftarrow \frac{\mathbf{g}}{\sqrt{g_1^2 + g_2^2 + g_3^2}}. \end{equation*}

Only triplets yielding non-negative gains are retained.

VBAP Limitations

  • Convex loudspeaker layouts are assumed (Pulkki, 1997).

  • Exactly one panning base is active at a time.

  • Distance is not explicitly modeled.

References

1999

  • Ville Pulkki. Uniform spreading of amplitude panned virtual sources. In Proceedings of the IEEE Workshop on Applications of Signal Processing to Audio and Acoustics, 187–190. 1999.
    [details] [BibTeX▼]

1997