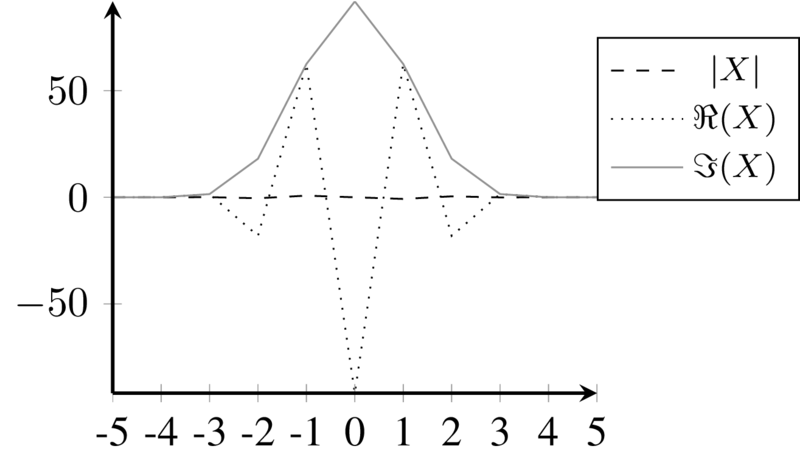
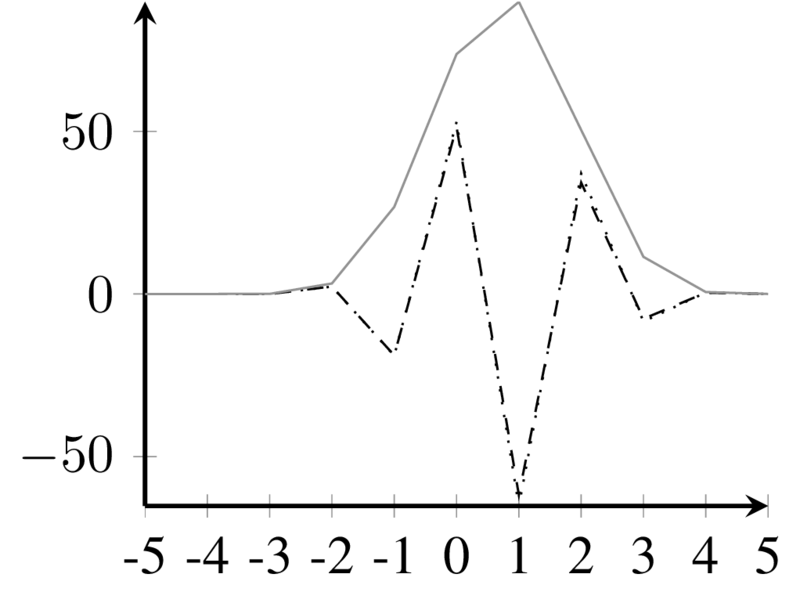
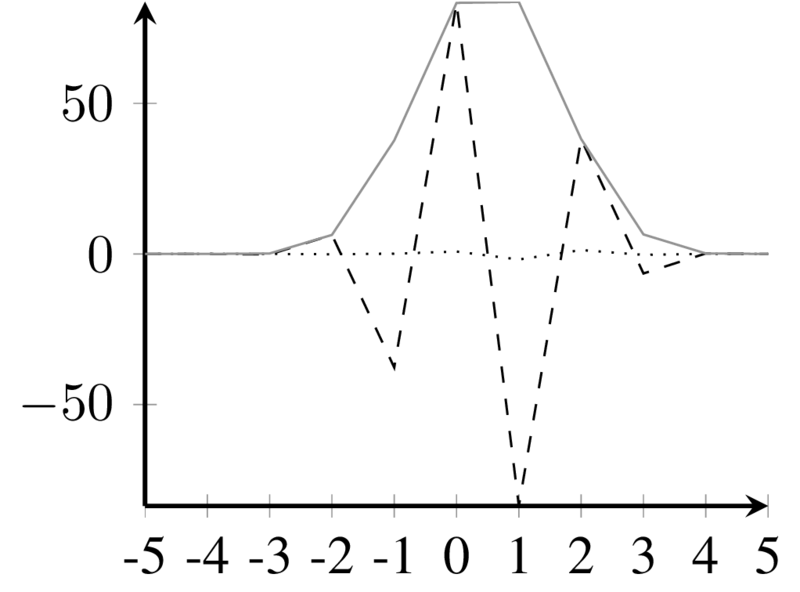
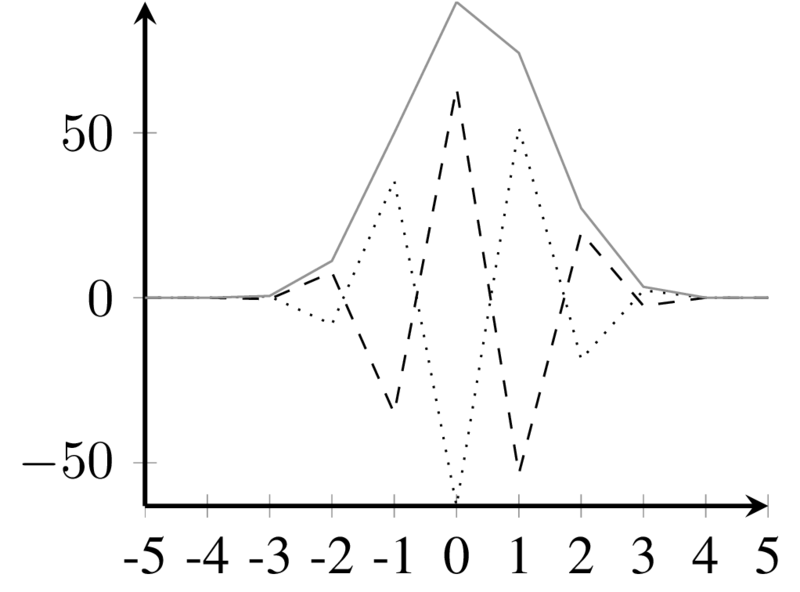
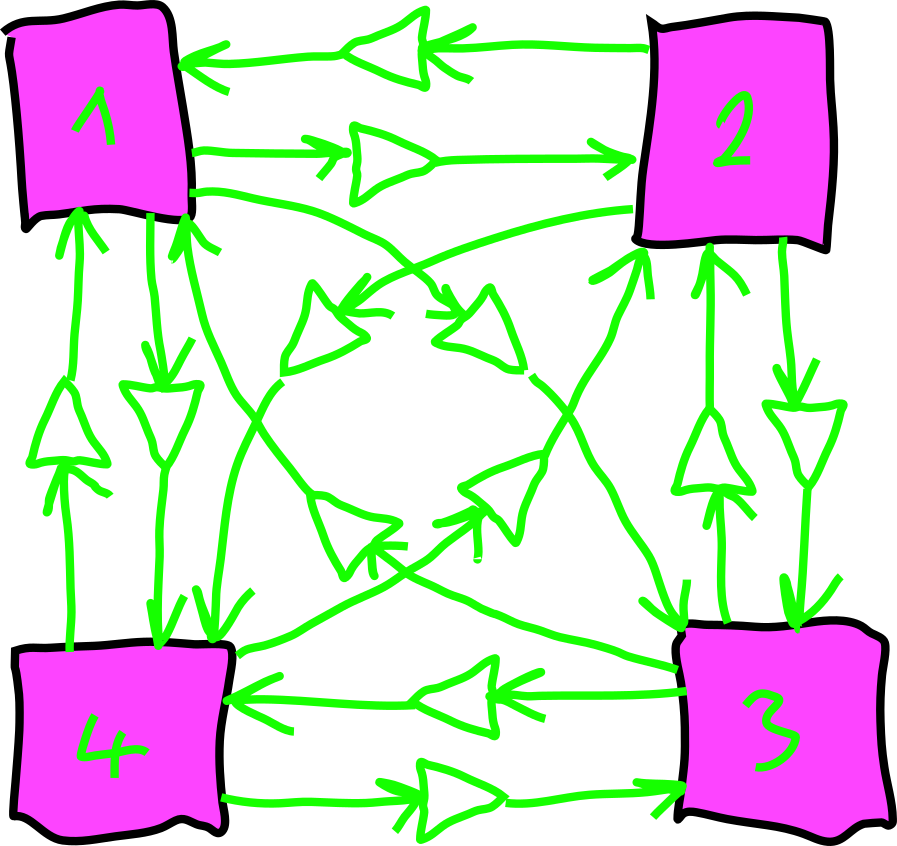
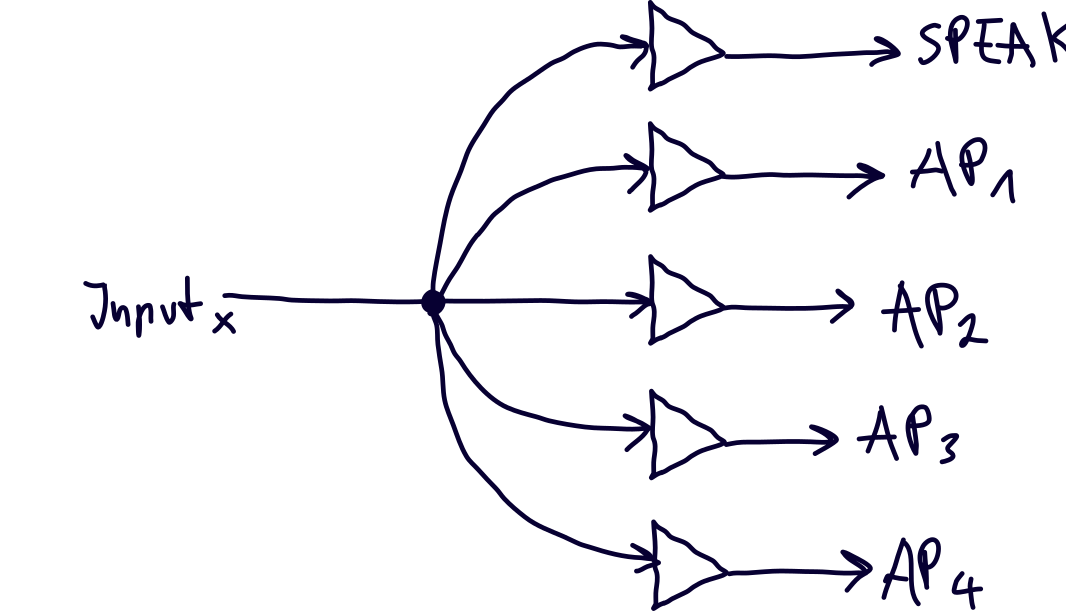
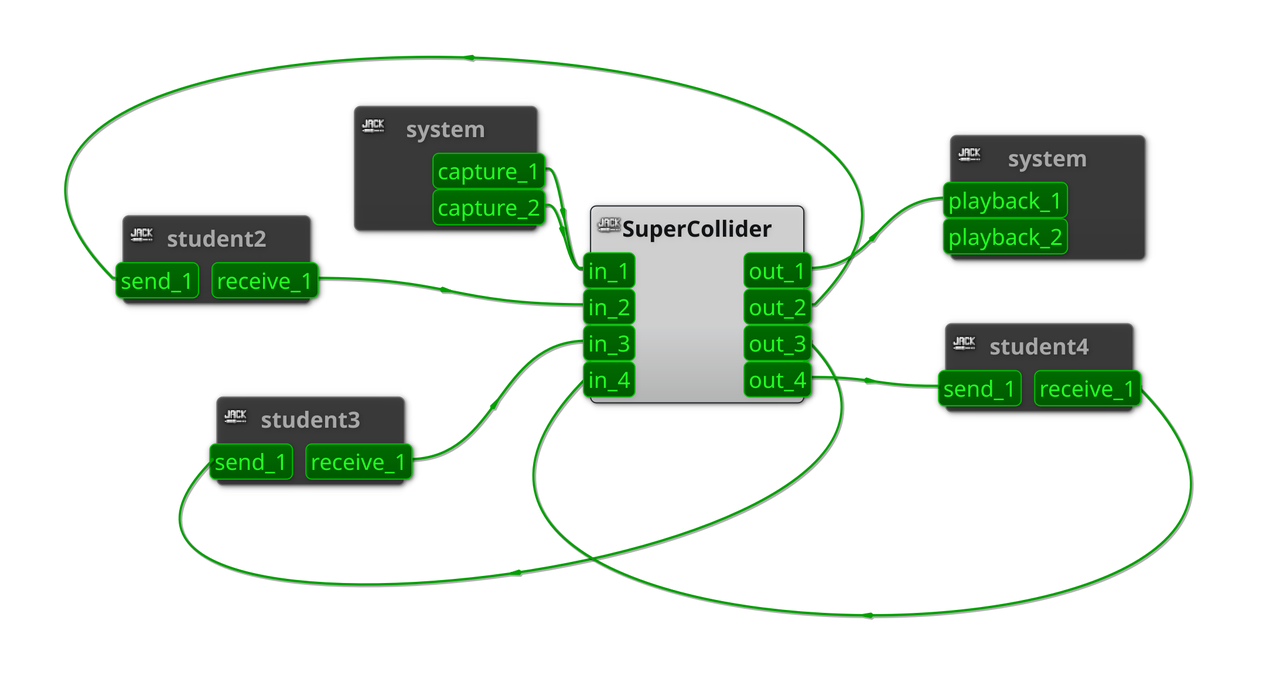
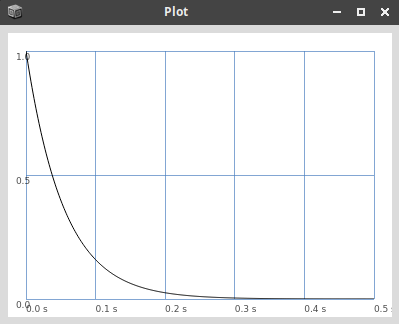
---------------------------------------------------------------------------
ModuleNotFoundError Traceback (most recent call last)
Cell In[2], line 1
----> 1 get_ipython().run_line_magic('run', 'header.ipynb')
File /media/anwaldt/ANWALDT_DATA/WORK/TEACHING/Online/RingBuffer/py-env/lib/python3.12/site-packages/IPython/core/interactiveshell.py:2480, in InteractiveShell.run_line_magic(self, magic_name, line, _stack_depth)
2478 kwargs['local_ns'] = self.get_local_scope(stack_depth)
2479 with self.builtin_trap:
-> 2480 result = fn(*args, **kwargs)
2482 # The code below prevents the output from being displayed
2483 # when using magics with decorator @output_can_be_silenced
2484 # when the last Python token in the expression is a ';'.
2485 if getattr(fn, magic.MAGIC_OUTPUT_CAN_BE_SILENCED, False):
File /media/anwaldt/ANWALDT_DATA/WORK/TEACHING/Online/RingBuffer/py-env/lib/python3.12/site-packages/IPython/core/magics/execution.py:741, in ExecutionMagics.run(self, parameter_s, runner, file_finder)
739 with preserve_keys(self.shell.user_ns, '__file__'):
740 self.shell.user_ns['__file__'] = filename
--> 741 self.shell.safe_execfile_ipy(filename, raise_exceptions=True)
742 return
744 # Control the response to exit() calls made by the script being run
File /media/anwaldt/ANWALDT_DATA/WORK/TEACHING/Online/RingBuffer/py-env/lib/python3.12/site-packages/IPython/core/interactiveshell.py:3005, in InteractiveShell.safe_execfile_ipy(self, fname, shell_futures, raise_exceptions)
3003 result = self.run_cell(cell, silent=True, shell_futures=shell_futures)
3004 if raise_exceptions:
-> 3005 result.raise_error()
3006 elif not result.success:
3007 break
File /media/anwaldt/ANWALDT_DATA/WORK/TEACHING/Online/RingBuffer/py-env/lib/python3.12/site-packages/IPython/core/interactiveshell.py:308, in ExecutionResult.raise_error(self)
306 raise self.error_before_exec
307 if self.error_in_exec is not None:
--> 308 raise self.error_in_exec
[... skipping hidden 1 frame]
File /tmp/ipykernel_22249/705522950.py:2
1 #%matplotlib notebook
----> 2 get_ipython().run_line_magic('matplotlib', 'inline')
4 from matplotlib import patches
6 import numpy as np
File /media/anwaldt/ANWALDT_DATA/WORK/TEACHING/Online/RingBuffer/py-env/lib/python3.12/site-packages/IPython/core/interactiveshell.py:2480, in InteractiveShell.run_line_magic(self, magic_name, line, _stack_depth)
2478 kwargs['local_ns'] = self.get_local_scope(stack_depth)
2479 with self.builtin_trap:
-> 2480 result = fn(*args, **kwargs)
2482 # The code below prevents the output from being displayed
2483 # when using magics with decorator @output_can_be_silenced
2484 # when the last Python token in the expression is a ';'.
2485 if getattr(fn, magic.MAGIC_OUTPUT_CAN_BE_SILENCED, False):
File /media/anwaldt/ANWALDT_DATA/WORK/TEACHING/Online/RingBuffer/py-env/lib/python3.12/site-packages/IPython/core/magics/pylab.py:103, in PylabMagics.matplotlib(self, line)
98 print(
99 "Available matplotlib backends: %s"
100 % _list_matplotlib_backends_and_gui_loops()
101 )
102 else:
--> 103 gui, backend = self.shell.enable_matplotlib(args.gui)
104 self._show_matplotlib_backend(args.gui, backend)
File /media/anwaldt/ANWALDT_DATA/WORK/TEACHING/Online/RingBuffer/py-env/lib/python3.12/site-packages/IPython/core/interactiveshell.py:3665, in InteractiveShell.enable_matplotlib(self, gui)
3662 import matplotlib_inline.backend_inline
3664 from IPython.core import pylabtools as pt
-> 3665 gui, backend = pt.find_gui_and_backend(gui, self.pylab_gui_select)
3667 if gui != None:
3668 # If we have our first gui selection, store it
3669 if self.pylab_gui_select is None:
File /media/anwaldt/ANWALDT_DATA/WORK/TEACHING/Online/RingBuffer/py-env/lib/python3.12/site-packages/IPython/core/pylabtools.py:338, in find_gui_and_backend(gui, gui_select)
321 def find_gui_and_backend(gui=None, gui_select=None):
322 """Given a gui string return the gui and mpl backend.
323
324 Parameters
(...)
335 'WXAgg','Qt4Agg','module://matplotlib_inline.backend_inline','agg').
336 """
--> 338 import matplotlib
340 if _matplotlib_manages_backends():
341 backend_registry = matplotlib.backends.registry.backend_registry
ModuleNotFoundError: No module named 'matplotlib'