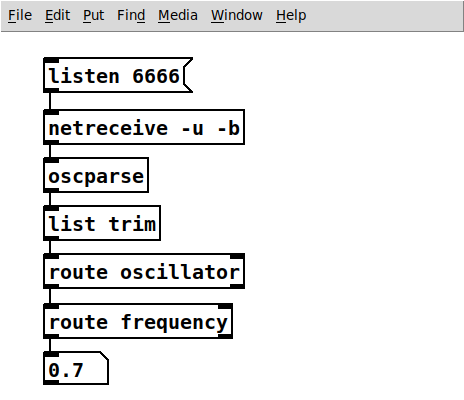
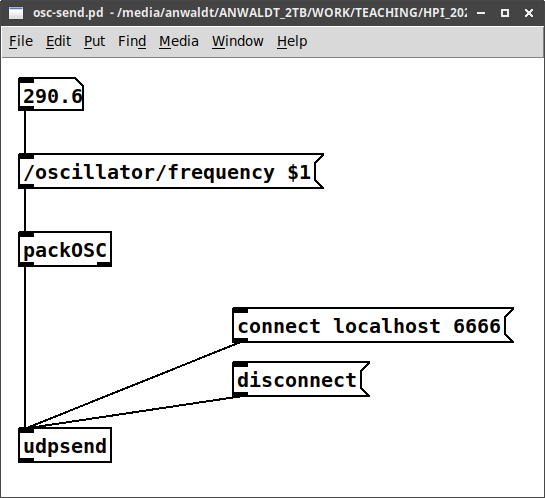
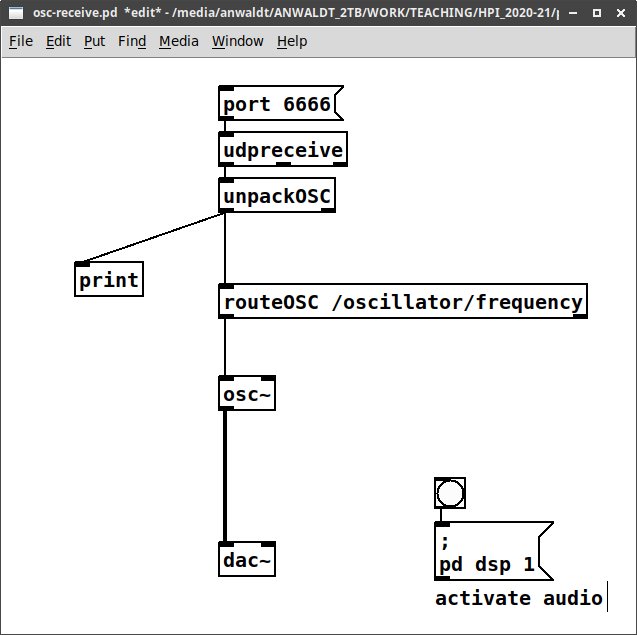
Git is a distributed version control system. Changes to (text) files are grouped in
chunks called commits. You can create new branches of a repository for specific
features or tasks and merge those branches after you finished your changes.
Cloning a Git Repository
git clone https://github.com/anwaldt/SPRAWL.git
This creates a directory with the name SPRAWL and clones the git repository locally.
With git log you can see all recent commits.
Create Branches, Adding Changes and Committing
Let's create a new branch for our changes:
git checkout -b new_changes
Now we are on a new created branch called new_changes. If you omit the -b
you checkout a branch that is on the remote repository.
The easiest way to committing changes is to commit every changes of files.
git add file.txt
git add file2.txt
git commit -m "Fixes wording of file.txt and file3.t wsgh s"
Sometimes it happens that you commited your changes too early but didn't pushed
your changes to the remote server.
If you only want to change the commit message you can use git commit --amend.
The same command works for adding more changes to the last commit.
Don't forget to use git add filename.
Pushing Changes to the Remote Server
With git you can have more than one remote repository. After you cloned the
sprawl repository you will have a remote repository with the name origin.
student@h2912420:~/SPRAWL$ git remote -v
origin https://github.com/anwaldt/SPRAWL.git (fetch)
origin https://github.com/anwaldt/SPRAWL.git (push)
But you don't have any push access to this repository. To get your changes
into the mainline SPRAWL repository you have to fork the project on github.
At the right top corner at the sprawl's repo
you must click on fork. Then you can add your own repo to your local SPRAWL clone:
$ git remote add ntonnaett https://github.com/ntonnaett/SPRAWL.git
$ git remote -v
ntonnaett https://github.com/ntonnaett/SPRAWL.git (fetch)
ntonnaett https://github.com/ntonnaett/SPRAWL.git (push)
origin git@github.com:anwaldt/SPRAWL.git (fetch)
origin git@github.com:anwaldt/SPRAWL.git (push)
Exchange ntonnaett with your personal remote name.
After you committed all your changes you can open a pull request on the mainline
sprawl repository.