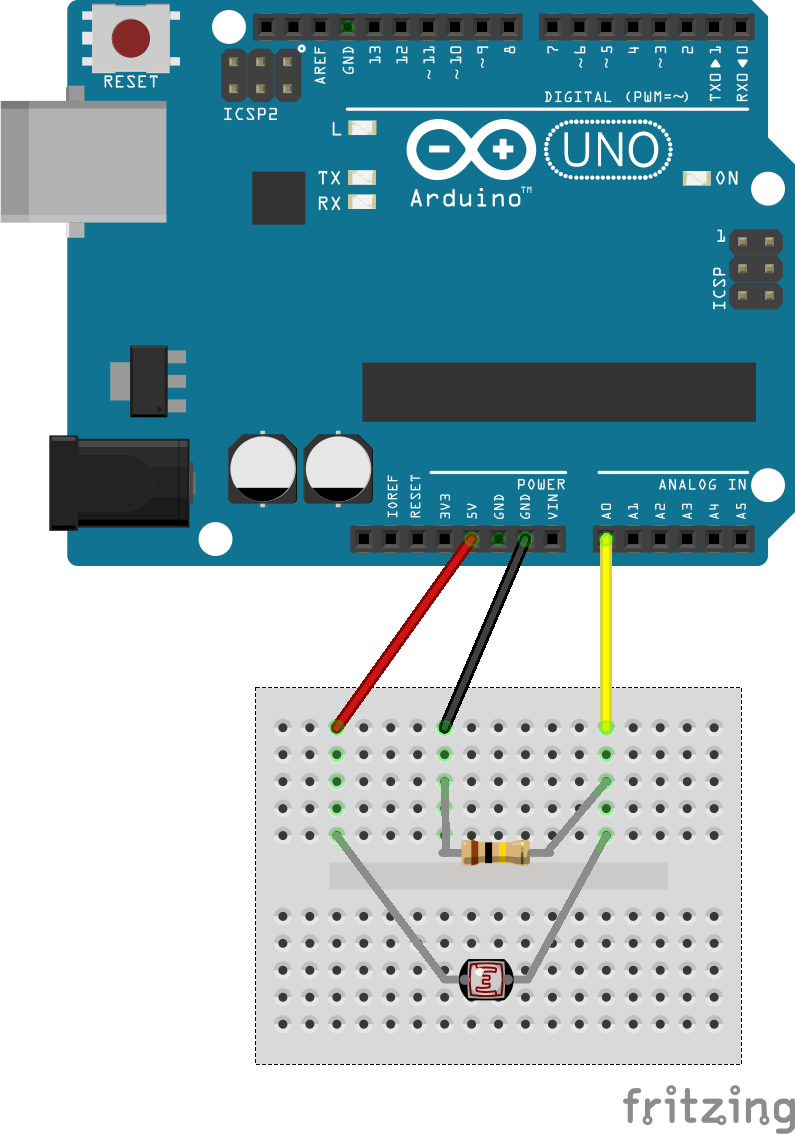
systemd is a set of tools managing, among other things, the startup procedure on Linux systems.
Within the Linux user and developer community, there is a debate whether systemd violates the Unix philosophy - however, it works well for starting all the software components we need when booting the server or the Access Points.
System services can be started in dependence on other services,
This makes it possible to start a system with many interrelations.
They can be started and stopped during operation.
Depending on the configuration, the services can also be restarted automatically if they crash.
Creating Services
systemd services can be declared as user services or system services.
They are defined in text files, which need to be located in one of the the following directories:
/usr/lib/systemd/user
/usr/lib/systemd/system
The JACK Service
The JACK service needs to be started before all other audio
applications, since they rely on a running JACK server.
A file jack.service defines the complete service:
[Unit]
Description=Jack audio server
After=sound.target local-fs.target
[Install]
WantedBy=multi-user.target
[Service]
Type=simple
PrivateTmp=true
Environment="JACK_NO_AUDIO_RESERVATION=1"
ExecStart=/usr/bin/jackd -P 90 -a a -d dummy -p 128
LimitRTPRIO=95
LimitRTTIME=infinity
LimitMEMLOCK=infinity
User=studio
JACK must be run as a normal user. The file above describes a system service
that starts jack as user studio.
But only administrators are allowed to control system services. If we want to
control a service as a normal user we need a user service without the User=studio
entry.
Managing Services
Once the service files are in place, several simple commands
are available for controlling them. They differ, depending on
whether a user service or system service is controlled.
The following examples refer to the JACK user service.
Controlling system services requires root privileges and
do not need the --user flag.
Starting a Service
systemctl --user start jack.service
Stopping a Service
systemctl --user stop jack.service
Activating a Service
Activating a service creates a symlink in ~/.config/systemd/user/multi-user.target.wants/jack.service, pointing to the original
file /usr/lib/systemd/user/jack.service.
Afterwards, the system is launched after the first login of the user and stopped after the last user session exits.
systemctl --user enable jack.service
Deactivating a Service
systemctl --user disable jack.service
Getting a Service's Status
The following command prints a system's status:
systemctl --user status jack.service
When the JACK sevice has been started sucessfully,
the output looks as follows:
● jack.service - Jack audio server
Loaded: loaded (/usr/lib/systemd/user/jack.service; enabled; vendor preset: enabled)
Active: active (running) since Tue 2021-04-13 23:00:14 BST; 3s ago
Main PID: 214518 (jackd)
CGroup: /user.slice/user-1000.slice/user@1000.service/jack.service
└─214518 /usr/bin/jackd -P 90 -a a -d dummy -p 256
Start user service on boot
Sometimes it is practical to have a user session running after the last session closes.
For example if you access a server only via SSH. To achieve this we have to set
the specific user to be lingering. This user's services will start at boot and quit at
shutdown now.
# loginctl enable-linger studio